快速排序是目前应用最广泛的排序算法，实现简单，而且对应各种不同的输入数据都有良好的性能，这篇文章就是介绍一下快速排序的实现

快速排序

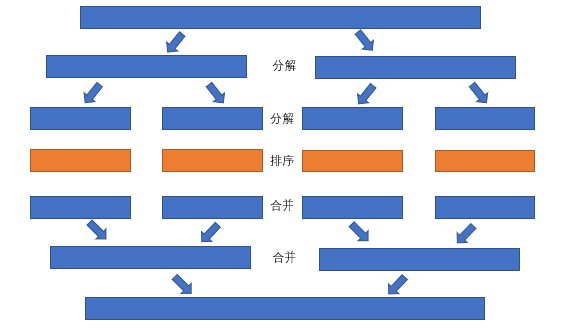
快速排序和归并排序有互通之处，都是使用了分治的思想，归并排序是将大数组分为两个小数组，当两个小数组排序好了以后，再进行合并，而快速排序则是将大数组以某个中间值分为两个数组，当两个小数组都有序，那么大数组也就有序了

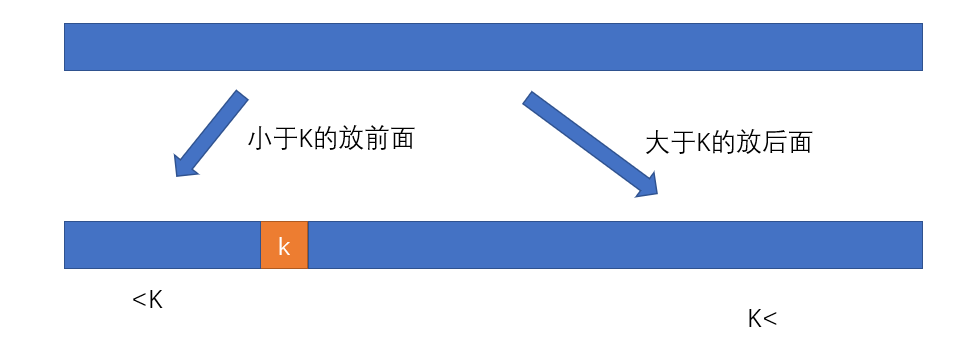
一般都是取数组的第一个元素来做拆分，然后递归向下拆分、排序，最终实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

function fastSort(arr, start = 0, end = arr.length - 1){
    if (end - start <= 0) return arr

    let k = arr[start]
    let i = start + 1, j = end
    while (true){
        while (arr[i] < k) i++

        while (k < arr[j]) j--

        if (i >= j) break
        [arr[i], arr[j]] = [arr[j], arr[i]]
    }
    [arr[start], arr[j]] = [arr[j], arr[start]]

    FastSort(arr, start, j - 1)
    FastSort(arr, j + 1, end)

    return arr
}

数组切分

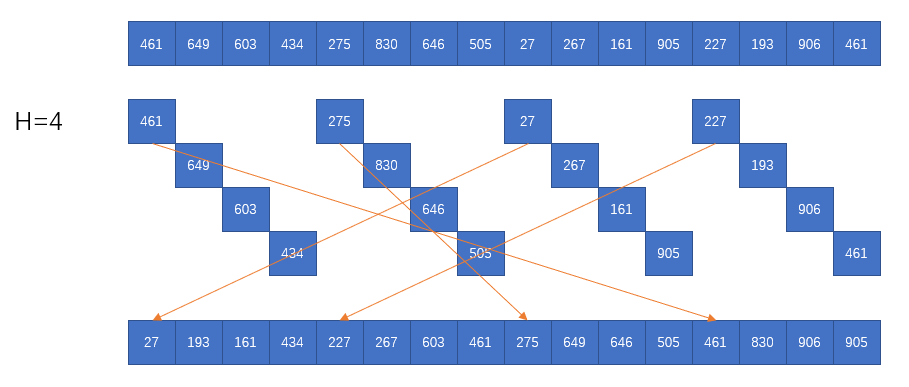
在快速排序中，数组的切分是比较核心的一部分，在通常算法下，都是选取切分部分的第一个元素作为切分的中间值，使用两个标记，一个从左到右，一个从右到左，左边的标记在寻到大于中间值的元素后停下，与右边的标记寻到的小于中间值的位置数据进行交换，循环下去，知道两个标记相遇

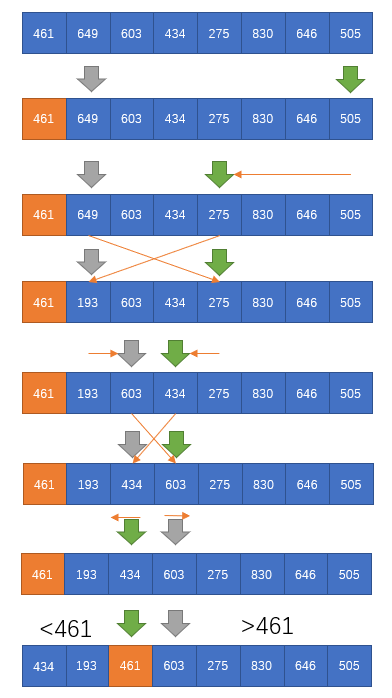
算法改进

1. 小数组使用插入排序

   这一点和归并排序相同，在数组较小时，递归的性能消耗较大，可以使用插排、选排这些算法对小数组进行排序

2. 三取样切分

   在一般情况下，切分的值都是取的第一个值，这个在遇到一些特殊情况的时候效率较低，所以取数组的中位数来切分才是最好的，但是计算中位数的代价也很高，所以可以从数组中随机取几个值，然后取其中的中位数，来实现，取样的大小可以是3、也可以是5

   

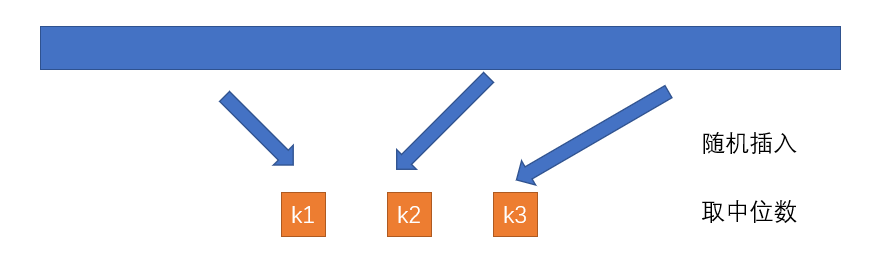
3. 三向切分

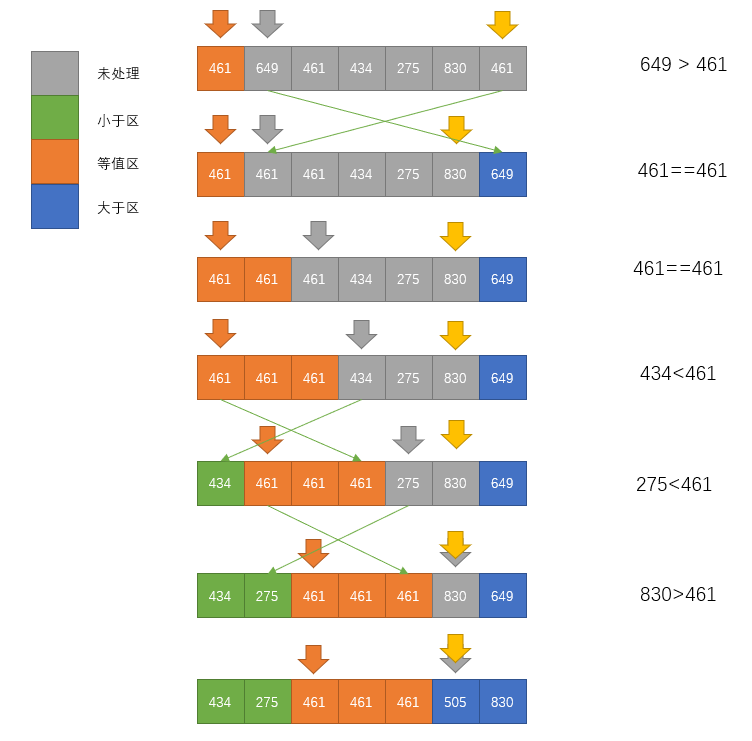
   在排序中可能遇到含有大量相等元素的情况，普通的切分方式会对包含有完全相同的数组继续进行递归切分，这部分操作是无意义的，可以通过算法来解决，也就是三向切分的快速排序

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

   function fastSort_3(arr, start = 0, end = arr.length - 1){ if (end - start <= 0) return arr let k = arr[start] let left = start, mid = start + 1, right = end while (mid <= right){ if (arr[mid] < k){ [arr[left], arr[mid]] = [arr[mid], arr[left]] left++ mid++ } else if (arr[mid] > k){ [arr[right], arr[mid]] = [arr[mid], arr[right]] right-- } else { mid++ } } fastSort_3(arr, start, left - 1) fastSort_3(arr, right + 1, end) return arr }

   这个展示的是Dijkstra的解法，感觉类似于冒泡，使用了3个标记来标记位置，其中left标记了小于切分值的数据下一次可以交换的位置，其实也就是切分值数组的左边，而mid则标记的切分值数组的右边，right这是标记的大于切分值的数组的最小边界，用于将扫描到的大于切分值的数据交换过去

   

算法属性

END

2019-02-27 完成

2019-02-25 立项

上一篇文章展示了4个容易理解的排序算法，这一篇继续讲述另一个排序算法—归并排序

归并排序

归并排序的核心思想就是分治，将一个数组拆分成2个小的数组，进行排序，排序完后进行合并

如果将元素分解到每个数组只有一个或者零个元素后，就不需要进行排序，直接进行合并就行了

自顶向下归并排序

归并排序可以自顶向下进行排序，也可以自底向上进行排序，两个的效率都差不多，其中自顶向下的排序的实现，是很典型的递归实现。是十分经典的分治

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

function mergeSort_top2bottom(arr, start, end){
    if (start === undefined && end === undefined){
        start = 0
        end = arr.length - 1
    }

    let cha = []
    function merge(arr, left, mid, right){
        let i = left, j = mid + 1

        for (let q = left; q <= right; q++){
            cha[q] = arr[q]
        }

        for (let q = left; q <= right; q++){
            if (i > mid) arr[q] = cha[j++]
            else if (j > right) arr[q] = cha[i++]
            else if (cha[i] <= cha[j]) arr[q] = cha[i++]
            else arr[q] = cha[j++]
        }
    }
    
    let len = end - start
    if (len <= 0) return

    let mid = parseInt((end + start) / 2)
    mergeSort_top2bottom(arr, start, mid)
    mergeSort_top2bottom(arr, mid + 1, end)
    merge(arr, start, mid, end)

    return arr
}

自底向上的归并排序

自底向上就是从长度为1的小数组开始，然后2,4,8,16…这样想上归并，最后形成一个大数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

function mergeSort_bottom2top(arr){
    let cha = []
    function merge(arr, left, mid, right){
        let i = left, j = mid + 1

        for (let q = left; q <= right; q++){
            cha[q] = arr[q]
        }

        for (let q = left; q <= right; q++){
            if (i > mid) arr[q] = cha[j++]
            else if (j > right) arr[q] = cha[i++]
            else if (cha[i] <= cha[j]) arr[q] = cha[i++]
            else arr[q] = cha[j++]
        }
    }

    let length = arr.length
    for (let base = 1; base >= arr.length; base *= 2){
        for (let i = 0; i < length; i = i + base * 2){
            merge(arr, i, i + base, Math.min(i + base * 2 - 1, length - 1))
        }
    }

    return arr
}

算法属性

分治算法还可以进行进一步的优化

1. 对小规模子数组使用插入排序

   归并排序使用递归的方式，在数组较小的时候频繁的递归调用函数对性能影响较大，所以当子数组的规模较小时，可以尝试使用其他排序算法(插入排序，选择排序)对子串进行排序，提升效率

2. 通过将排序数组和复制属性的身份互换的形式，减少复制数据的次数

END

2019-02-27 修复错误的算法复杂度

2019-02-25 完成

2019-02-25 立项

这里从排序算法开始说起，排序算法是很常见的需求，虽然在编程当中，排序大多使用已经封装好的函数，但还是需要深入了解一下

选择排序

排序当中，最容易理解和简单的就是选择排序了，算法就是首先在数组中找到最小的元素，然后将它与数组的第一个元素交换位置，接下来在剩下的元素中重复操作，直到完成排序

1
2
3
4
5
6
7
8
9
10
11
12
13

function selectSort(arr){
    let len = arr.length
    for (let i = 0; i < len; i++){
        let min = i
        for (let j = i + 1; j < len; j++){
            if (arr[min] > arr[j]){
                min = j
            }
        }
        [arr[i], arr[min]] = [arr[min], arr[i]]
    }
    return arr
}

算法属性

在这里有个稳定性的属性，稳定性指的是如果a=b，a初始在b的前面，那么排序完成后a依然在b的前面，如果不能保证a还是在b的前面，那么就是不稳定的

通过算法可以很容易看出，需要执行的操作都是稳定在1+2+3...+(n-1)，也就是n²/2，无论数据如何都是这样，而排序算法由于不是挨着交换，就可能导致跳过中间相等的元素，所以结果是不稳定的

插入排序

插入排序也想对很好理解，就是一个个的插入到合适的位置当中，就和拿扑克牌一样，算法就是从没有排好顺序的剩余数据中选择第一个，然后在已经排好顺序的数据中，从后向前查找，找到比它小的数据的时候，将其插入到这个数据的后面，后面的数据的位置整体+1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

function insertSort(arr){
    let len = arr.length
    for (let i = 1; i < len; i++){
        let j = i - 1
        
        for (; j >= 0; j--){
            if (arr[j] < arr[i]){
                break
            }
        }
        j++

        let data = arr[i]
        for (; j <= i; j++){
            [data, arr[j]] = [arr[j], data]
        }
    }
    return arr
}

算法属性

这个的平均时间复杂度和最差复杂度很容易看出来是O(n²)级别的，当数据就是排好序的时候，就不需要交换就处理完了

冒泡排序

冒泡排序和插入排序有些相似，所以常常被弄的很迷糊，冒泡排序同样也是一个个的选入然后放入排好序的队列当中，但是不想插排那样遍历找到合适的位置插入，而是和相邻的元素交换，知道前面的元素比自己大，这样一个个的向前交互的过程，就像一个个的泡泡上冒，说以叫做冒泡排序

1
2
3
4
5
6
7
8
9
10
11
12
13

function bubbleSort(arr){
    let len = arr.length
    for (let i = 1; i < len; i++){
        for (let j = i - 1; j >= 0; j--){
            if (arr[j] < arr[j + 1]){
                break
            }

            [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
        }
    }
    return arr
}

算法属性

冒泡的编码相对于插排来说要简单的多，但是由于需要挨个挨个的交换，这个会浪费大量的性能，所以大多采用插排而不是冒泡

希尔排序

希尔排序是一种基于插入排序的改进算法，在插入算法中，每个元素都需要从最后慢慢的遍历到前面来查找合适的位置，但是在数据量极大的时候，如果一个元素的位置很考前，那么就会遍历很久才能找到合适的位置，希尔排序的目标就是加速这一个过程，从而实现加速

希尔排序的思想是让数组中的数据在一定间隔h上是有序的，这样的数组被称为h有序数组，也就是说将h有序数组的元素，从任意位置上取出间隔h的数据组成的数组是有序的，希尔排序便是将数组从一个很大的h来排序，然后递减知道h=1就完成了排序，而希尔排序中用的h的递增数列是有相关研究的，有的算法会自动生成序列，有的则在外部存储了固定的序列，来加速

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

function shellSort(arr){
    let len = arr.length
    let h = 1
    //生成h
    while (h < (len - 1) / 3) h = 3 * h + 1

    while (h >= 1){
        for (let i = 1; i < len; i++){
            let j = i - h
            
            for (; j >= 0; j = j - h){
                if (arr[j] < arr[i]){
                    break
                }
            }
            j = j + h
    
            let data = arr[i]
            for (; j <= i; j = j + h){
                [data, arr[j]] = [arr[j], data]
            }
        }
        h = parseInt(h / 3)
    }
    return arr
}

算法属性

希尔排序在面对大数据量的时候，优势更加明显

END

2019-02-22 立项

2019-02-10 立项

前面讲了基础的数据结构,而算法作为程序的灵魂,对同样的事情拥有不同的操作,那么如何比较不同的算法之间,哪个的效率好,哪个的空间更省就需要用到算法分析相关的知识

算法分析

算法分析简单的就是分析一个算法运行需要多少时间以及需要多少内存,通常主要就是分析出算法的时间效率和空间效率

时间效率/时间复杂度

时间效率,也就是时间复杂度,例如在一个长度为n的数据中找到一个符合条件的值,最简单的就是直接遍历数组，通过这样的算法找到目标值的期望为(n + 1) / 2，这个值便是遍历查找的是时间效率

例如下图有个含有1-7的数组,现在需要从中找到6

现在开始查找,从左到右依次查找,经过6次后就招到了,这里执行的操作便是6次

但是查找的次数和数据量的大小、查找的目标数据的位置有关，当数据无穷大的时候，数据的位置随机的时候，如何对一个算法的效率进行估计呢？

这个算法的运气最好的时候的效率，当然是一下就找到了，也就是T(n)=1,当然也有最倒霉的时候，将数据遍历完了才找到需要的数据T(n)=n,在遍历中查找我们可以获取,

这里的运气最好的情况被称为最优时间复杂度，用Ω(n)来表示，意味着在数据量为n的情况下，算法运行时间至少是Ω(n)

这里的运气最差的情况被称为最差时间复杂度，用O(n)来表示，意味这在数据量为n的情况下，算法运行时间最多是O(n)

除此以外当然还有一个居中的平均时间复杂度，通Θ(n)来表示，这个表示的算法运行的期望时间

例如上面提到的遍历查找算法的效率就是Ω(n)=1, Θ(n)=(n + 1) / 2, O(n)=n,但在n特别大的时候，不同的量级之间的差距很小，较小的量级都可以忽略掉，例如(n+1)/2就可以简写未n/2,同时一般还会省去常量，所以Θ(n)=(n + 1) / 2可以写为Θ(n)≈n

对算法进行分析如何估算，也很简单，特别是通过代码来估算算法的复杂度，一般每多一层循环就需要多一个量级，比如一层循环就是n，两层循环就是n^2，以此类推，而其他的普通操作都是O(n)级别的，而递归则更容易导致对数级的复杂度log(n)、2^n

空间效率/空间复杂度

空间效率，也就是空间复杂度其实表示规则和时间效率相同，空间复杂度需要注意的是

1. 空间复杂度通常不计入原始输入本身所占用的空间大小
2. 空间复杂度主要记录这个算法自身需要的空间大小
3. 在算法递归中，递归也是要消耗空间的，过多的递归也会占据不可忽视的空间

量级

这里给出大小从低到高的一些常见量级，这个表也能在《算法（第四版）》中的117页找到

|描述|数量级|说明|举例|
|—|—|—|—|—|
|常数级别|1|普通语句|两数相加|
|对数级别|logN|二分策略|二分查找|
|线性级别|N|循环|找出最大的元素|
|线性对数级别|NlogN|分治|归并排序|
|平方级别|N^2|双重循环|检查所有元素对|
|立方级别|N^3|三重循环|检查所有三元组|
|指数级别|2^N|穷举查找|检查所有子集|

END

2019-02-21 立项

2019-01-18 立项

在现代的计算计中,数据都是通过线性的01进行存储和表示的,是一维线性的,所以最基础的数据结构也是一维线性的,多么复杂的数据结构都是从一维数据通过算法呈现出更加复制的功能的,这篇文章主要介绍数组以及链表这两个基础的数据结构

数组

数组是极其基础的数据结构，它通常具有固定的存储空间，是数据集合的最基础的一种结构

队列

队列的特性是先进先出,最先进入的元素将被最先处理

队列由于是从头部出栈,所以如果一直保持头部元素在最前面的话,每次出列对元素位进行维护需要耗费大量的操作,所以可以通过存储当前头部元素的位置来进行优化,保证每次操作与队列的容量无关

每次进行位置交换的方法

使用存储头部元素位置的方式

栈

栈也叫下压栈，特性与队列相反，是先进后出，最先进来的会在最后被处理

栈的数据结构由于加入和推出的操作都在最近操作的元素，所以记住整个栈的元素数量就行了比较简单，在这里就不弄多了

链表

数组是一段连续的空间，但是在现实中是不存在无限大的空间的，存储的空间往往出现不足以放下需要的数据的情况，或者申请了空间后不能在灵活的伸缩，链表通过则是通过指向其他空间的方式来将各个空间串联起来解决空间有限的问题

链表虽然会额外花费指向其他存储空间地址的资源，但是可以将零散的数据空间充分的利用起来。

===

虽然链表和数组很简单，但是数据和链表是最基础的数据结构，通过它们可以构建出更加复杂的数据机构，图、树等等

END

2019-02-19 加入了对链表的介绍

2019-02-17 完成

2019-01-18 立项

为了保证github的小绿点，每天都要写代码提交一波，但是有的时候确实有事啊，或者写了代码忘了提交，就会丢掉好不容易积累起来的小绿点，这篇文章简单介绍一下如何设置git提交记录的提交时间，git提交设定时间再也不怕小绿点没了~~~！

git commit –date

设置是时间的方式就是commit命令使用date属性来设置，例如下面的命令，可以看到提交历史里面，时间是设定的时间

获取时间戳

git支持的时间戳格式有3种，可以在git 提交日期格式规范里面找到，其中最简单的就是2005-04-07T22:13:13这样的格式，下面可以看到我们将日期设置到了2020年也是可以的~~~！

PS:时间是不能低于上次提交的时间的，不然就会无效

参考资料

git commit 官方手册

git 提交日期格式规范

git 修改上次git commit的时间

END

2019-02-13 完成

2019-01-06 立项

每次打TAG都要跑去远程仓库很麻烦，如果可以本地打就好了，这篇文章讲述如何使用git命令本地打TAG

准备

在这之前先在线上git仓库创建一个工程，然后clone下来，并进行一次提交

查看和设置TAG

首先中使用git tag -l查看已有的TAG，当然一个空工程刚开始是没有的，这里我们使用git tag <tagname>来设置一个叫test的TAG，设置后再次查看就可以看到设置的TAG了~~

删除TAG

如果想要删除本地的一些TAG，可使用git tag -d <tagname>的方式来删除

推送TAG

在本地设置好以后，有些时候会想把它推送到线上，比如版本号之类的，这里可以使用git push <remote> <tagname>的方式来推送

推送后，就可以在线上看到了

TAG附加信息

TAG一般还会附加上备注信息，只需要加上-m <msg>就行，也就是git tag <tagname> -m <msg>

参考资料

git tag 命令官方文档

END

2019-02-09 完成

2019-02-08 立项

新买了个服务器，需要安装doker，之前安装docker没有记录下来，这次记录一下安装以及配置源的过程~~~~

安装 Docker

根据官方文档，使用源的方式进行安装时最简单和便捷的

1. 执行命令更新源

   sudo apt-get update

2. 执行命令下载依赖

   sudo apt-get install apt-transport-https ca-certificates curl gnupg-agent software-properties-common

3. 执行命令添加docker官方GPG key

   curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo apt-key add -

   sudo apt-key fingerprint 0EBFCD88

   

4. 执行命令添加对应的源,其中的arch是系统CPU架构

   sudo add-apt-repository “deb [arch=amd64] https://download.docker.com/linux/ubuntu $(lsb_release -cs) stable”

5. 执行命令再次更新源

   sudo apt-get update

6. 执行命令安装docker

   sudo apt-get install docker-ce docker-ce-cli containerd.io

   

7. 安装完成~~~

   

安装docker-compose

docker-compose也是一个很重要的命令，我们继续安装docker-compose

1. 执行命令下载docker-compose

   sudo curl -L “https://github.com/docker/compose/releases/download/1.23.2/docker-compose-$(uname -s)-$(uname -m)” -o /usr/local/bin/docker-compose

   这里的1.23.2是docker-compose的版本号，可以根据情况咨询更换

2. 给下载的docker-compose程序赋予执行权限

   sudo chmod +x /usr/local/bin/docker-compose

3. 安装完成

   

参考资料

官方ubuntu安装文档

官方docker-compose安装文档

END

2019-02-02 完成

2019-02-02 立项

很久没有学习和练习算法了，但算法作为程序的灵魂，数据结构作为程序的躯体，不能忘记，从这篇文章开始，后面我准备整理一下几年都没有接触和学习的算法和数据结构。这一次我将依靠《算法》这本书来进行。

算法

算法是程序的灵魂这句话相信学习了编程的人都一定听到过，算法代表的是一个解决方案精确且完整的描述，是一系列解决问题的清晰的指令，是对数据状态从一个状态转换到另一个状态的描述。

解决问题的过程，即解决问题一步一步的步骤就是算法。

而且一个算法需要满足有效性和终止性：

有效性：算法是有效的，需要给出满足目标的结果。

终止性：算法是可以在有限的时间内完成的，因为无限长的时间才能实现目标是没有意义的！

为什么学习算法？

在生活中我们对事情的处理过程，都是是通过一个个的步骤来实现，解决问题的过程也正是在执行一个个算法，但是仅仅通过生活中的事情来学习和总结”算法“是低效的，我们在生活中学习过去前辈们的经验来处理现实中遇到的难题，同样在程序中为了让程序更加高效的完成任务，也需要学习和总结的算法。

为此我们需要学习和总结算法，来编写一个更加高质量的高效的可靠的程序，同时学习算法的同时也是锻炼我们的逻辑思维的过程，锻炼我们将一个问题进行拆分，然后分步实现，最后组装的能力。

数据结构

一个程序是由算法和数据结构组成的，算法作为灵魂，那么数据结构就是程序的躯体，灵魂和躯体，缺一不可。

数据结构除了最基本的存储数据和表现数据的功能以外，它作为一种数据存储和组织的方式最大的用处在于提高运行效率或者存储效率。同时它也是算法的起始点、中间点以及结束点，算法的运行必然是在数据结构之上的。

常见的数据结构主要有：数组，背包，栈，队列，链表，树、、、等等

这些数据结构将在后面进行讲解

参考资料

百度百科_算法

百度百科_数据结构

END

2019-01-23 完成

2019-01-16 立项

本文简单讲述简单工厂模式

功能

简单工厂模式其实算不上设计模式，但是由于十分简单好用，所以经常被使用到，它是一种创建类的设计模式，对对象的创建进行的了封装

简单工厂模式也十分容易理解，就是传入一个容易理解的参数，来获取对应的复杂对象，就像工厂一样我想要什么，工厂就会给我生成什么出来

URL结构图

示例

工厂生产汽车

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

#include <iostream>
using namespace std;

//汽车类
class Car {
public:
    virtual void didi() {
        cout << "滴滴" << endl;
    }
};

class SedanCar :public Car {
public:
    virtual void didi() {
        cout << "滴滴 小轿车" << endl;
    }
};

class BigTruck :public Car {
public:
    virtual void didi() {
        cout << "滴滴 大卡车" << endl;
    }
};

//工厂类
class CarFactory {
public:
    Car * createCar(string carType) {
        if (carType == "Car") {
            return new Car();
        }
        else if (carType == "SedanCar") {
            return new SedanCar();
        }
        else if (carType == "BigTruck") {
            return new BigTruck();
        }
        else {
            return nullptr;
        }
    }
};

int main()
{
    Car * car;
    CarFactory carFactory;
    car = carFactory.createCar("Car");
    car->didi();
    car = carFactory.createCar("SedanCar");
    car->didi();
    car = carFactory.createCar("BigTruck");
    car->didi();
}

这个示例里面，使用工厂类来生成具体的汽车类，可以让客户端不需要知道具体的汽车类，只需要接触工厂

END

2018-12-06 完成

2018-12-05 立项